Maximum Mean Discrepancy#
(in progress)
Biased, squared maximum mean discrepancy#
Proposed by Gretton et al. (2012)
\(MMD_b^2 = \frac{1}{m^2} \sum_{i,j=1}^m k(x_i,x_j)-\frac{2}{mn}\sum_{i,j=1}^{m,n} k(x_i,y_j)+\frac{1}{n^2}\sum_{i,j=1}^n k(y_i,y_j)\)
Kernel choices#
Energy kernel#
Suggested by Feydy et al. (2019), Feydy (2020)
\(k(x,y) = -||x-y||\)
Gaussian kernel#
\(k(x,y) = \exp\left(-\frac{||x-y||^2}{2\sigma^2}\right)\) whereby \(||x-y||^2 = x^\top x - 2xy + y^\top y\)
Example: MMD with energy kernel#
\(MMD_b^2 = \frac{1}{m^2} \sum_{i,j=1}^m \underbrace{-||x_i-x_j||}_{A}-\frac{2}{mn}\sum_{i,j=1}^{m,n} \underbrace{-||x_i-y_j||}_{B}+\frac{1}{n^2}\sum_{i,j=1}^n \underbrace{-||y_i-y_j||}_{C}\) consider \(x, y\) to be column vectors.
Step 1: Compute the euclidean distance#
\[\begin{align*}
\textbf{A :} &-||x_i-x_j||= -\sqrt{ \left(||x_i-x_j||^2 \right)} = -\sqrt{\left( x_i x_i^\top - 2x_i x_j^\top + x_j x_j^\top \right)} \\
\textbf{B :} &-||x_i-y_j||=-\sqrt{\left(||x_i-y_j||^2\right)} = -\sqrt{\left(x_i x_i^\top - 2x_i y_j^\top + y_j y_j^\top\right)} \\
\textbf{C :} &-||y_i-y_j||=-\sqrt{\left(||y_i-y_j||^2\right)} = -\sqrt{\left(y_i y_i^\top - 2y_i y_j^\top + y_j y_j^\top\right)}
\end{align*}\]
Step 2: Compute the biased squared maximum mean discrepancy#
\(MMD_b^2 = \frac{1}{m^2} \sum_{i,j=1}^m A -\frac{2}{mn}\sum_{i,j=1}^{m,n} B +\frac{1}{n^2}\sum_{i,j=1}^n C\)
References:#
Feydy, J., Séjourné, T., Vialard, F. X., Amari, S. I., Trouvé, A., & Peyré, G. (2019, April). Interpolating between optimal transport and mmd using sinkhorn divergences. In The 22nd International Conference on Artificial Intelligence and Statistics (pp. 2681-2690). PMLR. PDF
Feydy, J. (2020). Geometric data analysis, beyond convolutions. Applied Mathematics, 3. PhD Thesis. PDF
Gretton, A., Borgwardt, K. M., Rasch, M. J., Schölkopf, B., & Smola, A. (2012). A kernel two-sample test. The Journal of Machine Learning Research, 13(1), 723-773. PDF
Implementation#
import numpy as np
import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions
class MMD2:
def __init__(self, kernel : str = "energy", sigma : int or None = None,
**kwargs):
"""
Computes the biased, squared maximum mean discrepancy
Parameters
----------
kernel : str
kernel type used for computing the MMD such as "gaussian", "energy"
The default is "energy".
sigma : int, optional
Variance parameter used in the gaussian kernel.
The default is None.
**kwargs : keyword arguments
Additional keyword arguments.
"""
self.kernel_name = kernel
self.sigma = sigma
def __call__(self, x, y):
"""
Computes the biased, squared maximum mean discrepancy of two samples
Parameters
----------
x : tensor of shape (batch, num_samples)
preprocessed expert-elicited statistics.
Preprocessing refers to broadcasting expert data to same shape as
model-simulated data.
y : tensor of shape (batch, num_samples)
model-simulated statistics corresponding to expert-elicited
statistics
Returns
-------
MMD2_mean : float
Average biased, squared maximum mean discrepancy between expert-
elicited and model simulated data.
"""
# treat samples as column vectors
x = tf.expand_dims(x, -1)
y = tf.expand_dims(y, -1)
# Step 1
# compute dot product between samples
xx = tf.matmul(x, x, transpose_b=True)
xy = tf.matmul(x, y, transpose_b=True)
yy = tf.matmul(y, y, transpose_b=True)
# compute squared difference
u_xx = self.diag(xx)[:,:,None] - 2*xx + self.diag(xx)[:,None,:]
u_xy = self.diag(xx)[:,:,None] - 2*xy + self.diag(yy)[:,None,:]
u_yy = self.diag(yy)[:,:,None] - 2*yy + self.diag(yy)[:,None,:]
# apply kernel function to squared difference
XX = self.kernel(u_xx, self.kernel_name, self.sigma)
XY = self.kernel(u_xy, self.kernel_name, self.sigma)
YY = self.kernel(u_yy, self.kernel_name, self.sigma)
# Step 2
# compute biased, squared MMD
MMD2 = tf.reduce_mean(XX, (1,2)) - 2*tf.reduce_mean(XY, (1,2)) + tf.reduce_mean(YY, (1,2))
MMD2_mean = tf.reduce_mean(MMD2)
return MMD2_mean, MMD2, XX, XY, YY
def clip(self, u):
u_clipped = tf.clip_by_value(u, clip_value_min=1e-8,
clip_value_max=int(1e10))
return u_clipped
def diag(self, xx):
diag = tf.experimental.numpy.diagonal(xx, axis1=1, axis2=2)
return diag
def kernel(self, u, kernel, sigma):
if kernel=="energy":
# clipping for numerical stability reasons
d=-tf.math.sqrt(self.clip(u))
if kernel=="gaussian":
d=tf.exp(-0.5*tf.divide(u, sigma))
return d
Example simulations#
Numeric toy example with one-dimensional samples \(X\sim N(0,0.05)\) and \(Y\sim N(1,0.08)\)#
# instance of MMD2 class
mmd2 = MMD2(kernel="energy")
# initialize batches (B), number of samples (N,M)
B = 40
N,M = (20,50)
# draw for samples from two normals (x,y)
x = tfd.Normal(loc=0, scale=0.05).sample((B,N))
y = tfd.Normal(loc=1, scale=0.08).sample((B,M))
# compute biased, squared mmd for both samples
mmd_avg, mmd_batch, A, B, C = mmd2(x,y)
# print results
print("Biased, squared MMD (avg.):\n", mmd_avg.numpy())
print(" ")
print("Biased, squared MMD (per batch):\n", tf.stack(mmd_batch).numpy())
print(" ")
print("A (shape): ", A.shape, ", A (mean): ", np.round(tf.reduce_mean(A).numpy(), 2))
print("B (shape): ", B.shape, ", B (mean): ", np.round(tf.reduce_mean(B).numpy(), 2))
print("C (shape): ", C.shape, ", C (mean): ", np.round(tf.reduce_mean(C).numpy(), 2))
Biased, squared MMD (avg.):
1.8592064
Biased, squared MMD (per batch):
[1.8778989 1.8725448 1.8520763 1.8433806 1.8375555 1.8706871 1.8377426
1.8460778 1.8356341 1.8626964 1.864194 1.8219937 1.8829894 1.8823482
1.9019922 1.8328006 1.9002373 1.8837405 1.8773578 1.8063233 1.8772355
1.818045 1.8549396 1.9211222 1.878836 1.8874218 1.8746109 1.8420508
1.8514216 1.8765984 1.8030391 1.8502506 1.8581074 1.8660026 1.868265
1.8145266 1.8823993 1.827515 1.8466772 1.8789287]
A (shape): (40, 20, 20) , A (mean): -0.05
B (shape): (40, 20, 50) , B (mean): -1.0
C (shape): (40, 50, 50) , C (mean): -0.09
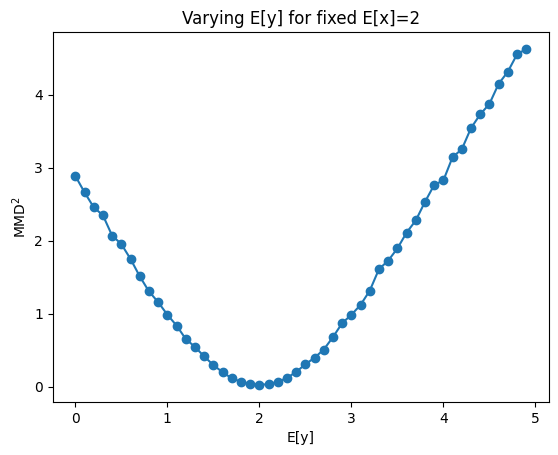
Behavior of \(MMD^2\) for varying differences between \(X\) and \(Y\)#
The loss is zero when X=Y otherwise it increases with stronger dissimilarity between X and Y
import matplotlib.pyplot as plt
mmd=[]
xrange=tf.range(0, 5, 0.1).numpy()
for m in xrange:
# instance of MMD2 class
mmd2 = MMD2(kernel="energy")
# initialize batches (B), number of samples (N,M)
B = 40
N,M = (50,50)
# draw for samples from two normals (x,y)
x = tfd.Normal(loc=2, scale=0.5).sample((B,N))
y = tfd.Normal(loc=m, scale=0.5).sample((B,M))
# compute biased, squared mmd for both samples
mmd_avg, *_ = mmd2(x,y)
mmd.append(mmd_avg)
plt.plot(xrange, mmd, "-o")
plt.ylabel(r"$MMD^2$")
plt.xlabel("E[y]")
plt.title("Varying E[y] for fixed E[x]=2")
plt.show()
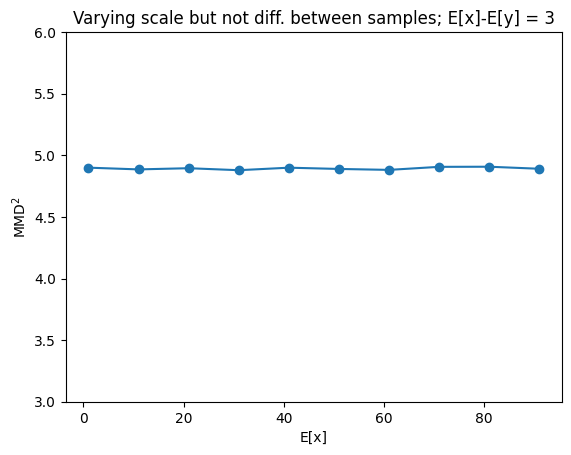
Behavior of \(MMD^2\) for varying scale but same difference between X and Y#
Changes in scale do not affect the loss value
mmd=[]
xrange=tf.range(1.,100., 10).numpy()
for x_m in xrange:
# instance of MMD2 class
mmd2 = MMD2(kernel="energy")
# initialize batches (B), number of samples (N,M)
B = 400
N,M = (50,50)
diff = 3.
# draw for samples from two normals (x,y)
x = tfd.Normal(loc=x_m, scale=0.5).sample((B,N))
y = tfd.Normal(loc=float(x_m-diff), scale=0.5).sample((B,M))
# compute biased, squared mmd for both samples
mmd_avg, *_ = mmd2(x,y)
mmd.append(mmd_avg)
plt.plot(xrange, mmd, "-o")
plt.ylabel(r"$MMD^2$")
plt.xlabel("E[x]")
plt.title("Varying scale but not diff. between samples; E[x]-E[y] = 3")
plt.ylim(3,6)
plt.show()
