Toy Example - Parametric prior

Toy Example - Parametric prior#

import tensorflow_probability as tfp
import matplotlib.pyplot as plt
import tensorflow as tf
import seaborn as sns
import pandas as pd
import numpy as np
import elicit as el

from elicit.extras import utils

tfd = tfp.distributions

The Model#

Generative model#

\[\begin{align*} \beta_0 &\sim \text{Normal}(\mu_0, \sigma_0) \\ \beta_1 &\sim \text{Normal}(\mu_1, \sigma_1) \\ \sigma &\sim \text{HalfNormal}(\sigma_2) \\ \mu &= \beta_0 + \beta_1X \\ y_{pred} &\sim \text{Normal}(\mu, \sigma) \end{align*}\]

Implementation#

Predictor#

# create a predictor ranging from 1 to 200 
# standardize predictor
# select the 25th (X0), 50th (X1), and 75th (X2) quantile of the std. predictor for querying the expert
def std_predictor(N, quantiles):
    X = tf.cast(np.arange(N), tf.float32)
    X_std = (X-tf.reduce_mean(X))/tf.math.reduce_std(X)
    X_sel = tfp.stats.percentile(X_std, quantiles)
    return X_sel
    
std_predictor(N=200, quantiles=[25,50,75])

<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-0.85737586,  0.00866036,  0.85737586], dtype=float32)>

Generative model#

class ToyModel2:
    def __call__(self, prior_samples, design_matrix, **kwargs):
        B = prior_samples.shape[0]
        S = prior_samples.shape[1]

        # preprocess shape of design matrix
        X = tf.broadcast_to(design_matrix[None, None,:],
                           (B,S,len(design_matrix)))
        # linear predictor (= mu)
        epred = tf.add(prior_samples[:, :, 0][:,:,None],
                       tf.multiply(prior_samples[:, :, 1][:,:,None], X)
                       )
        # data-generating model
        likelihood = tfd.Normal(
            loc=epred, scale=tf.expand_dims(prior_samples[:, :, -1], -1)
        )
        # prior predictive distribution (=height)
        ypred = likelihood.sample()
        
        # selected observations
        y_X0, y_X1, y_X2 = (ypred[:,:,0], ypred[:,:,1], ypred[:,:,2])

        # log R2 (log for numerical stability)
        log_R2 = utils.log_R2(ypred, epred)

        return dict(
            likelihood=likelihood,
            ypred=ypred, epred=epred,
            prior_samples=prior_samples,
            y_X0=y_X0, y_X1=y_X1, y_X2=y_X2,
            log_R2=log_R2
        )

Model input for elicit method#

# specify the model
model=el.model(
        obj=ToyModel2,
        design_matrix=std_predictor(N=200, quantiles=[25,50,75])
        )

Model parameters#

  • intercept with normal prior \(\beta_0\)

  • slope with normal prior \(\beta_1\)

  • random noise with halfnormal prior \(\sigma\)

To be learned hyperparameters \( \lambda = (\mu_0, \sigma_0, \mu_1, \sigma_1, \sigma_2) \)

  • scale parameters (\(\sigma_0, \sigma_1, \sigma_2\)) are constrained to be positive

Parameter input for elicit method#

parameters=[
        el.parameter(
            name="beta0",
            family=tfd.Normal,
            hyperparams=dict(
                loc=el.hyper("mu0"),
                scale=el.hyper("sigma0", lower=0)
                )
        ),
        el.parameter(
            name="beta1",
            family=tfd.Normal,
            hyperparams=dict(
                loc=el.hyper("mu1"),
                scale=el.hyper("sigma1", lower=0)
                )
        ),
        el.parameter(
            name="sigma",
            family=tfd.HalfNormal,
            hyperparams=dict(
                scale=el.hyper("sigma2", lower=0)
                )
        ),
    ]

Target quantities and elicitation techniques#

Target quantities

  • query expert regarding prior predictions \(y \mid X_{i}\) with \(i\) being the 25th, 50th, and 75th quantile of the predictor.

Elicitation technique

  • query each observation using quantile-based elicitation using \(Q_p(y \mid X)\) for \(p=5, 25, 50, 75, 95\)

Importance of elicited statistics in loss

  • all elicited statistics should have equal importance (weight=1.0)

  • for computing the discrepancy between expert-elicited statistics and model simulations with use the Maximum Mean Discrepancy with Energy kernel

Targets input for elicit method#

targets=[
    el.target(
        name="y_X0",
        query=el.queries.quantiles((5, 25, 50, 75, 95)),
        loss=el.losses.MMD2(kernel="energy"),
        weight=1.0
    ),
    el.target(
        name="y_X1",
        query=el.queries.quantiles((5, 25, 50, 75, 95)),
        loss=el.losses.MMD2(kernel="energy"),
        weight=1.0
    ),
    el.target(
        name="y_X2",
        query=el.queries.quantiles((5, 25, 50, 75, 95)),
        loss=el.losses.MMD2(kernel="energy"),
        weight=1.0
    ),
    el.target(
        name="log_R2",
        query=el.queries.quantiles((5, 25, 50, 75, 95)),
        loss=el.losses.MMD2(kernel="energy"),
        weight=1.0
    )
    ]

Expert elicitation#

  • instead of querying a “real” expert, we define a ground truth (i.e., oracle) and simulate the oracle-elicited statistics

Expert input for elicit method (here: oracle)#

# specify ground truth
ground_truth = {
    "beta0": tfd.Normal(loc=5, scale=1),
    "beta1": tfd.Normal(loc=2, scale=1),
    "sigma": tfd.HalfNormal(scale=10.0),
}

# define oracle
expert=el.expert.simulator(
        ground_truth = ground_truth,
        num_samples = 10_000
    )

Training: Learn prior distributions based on expert data#

All inputs for elicit method

elicit = el.Elicit(
    model=model,
    parameters=parameters,
    targets=targets,
    expert=expert,
    optimizer=el.optimizer(
        optimizer=tf.keras.optimizers.Adam,
        learning_rate=0.1,
        clipnorm=1.0
        ),
    trainer=el.trainer(
        method="parametric_prior",
        name="toy2",
        seed=1,
        epochs=400
    ),
    initializer=el.initializer(
        method="sobol",
        loss_quantile=0,
        iterations=32,
        distribution=el.initialization.uniform(
            radius=2.,
            mean=0.
            )
        )
)

# run method
hist = elicit.fit(save_dir=None)

Initialization

100%|██████████| 32/32 [00:06<00:00,  5.03it/s]

 
Training

100%|██████████| 400/400 [02:37<00:00,  2.54it/s]

Results#

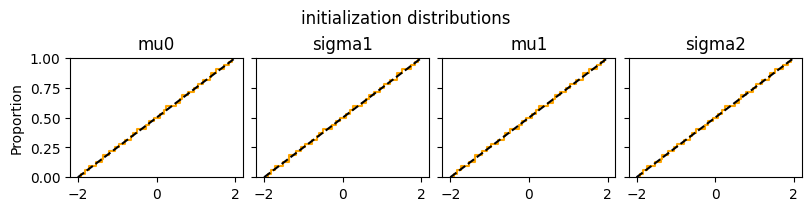
Initialization of hyperparameters#

def plot_inits(res):
    n_par = len(res["init_matrix"].keys())
    fig, axs = plt.subplots(1,n_par, figsize=(8,2), constrained_layout=True, sharex=True, sharey=True)
    for i,hyp in enumerate(res["init_matrix"]):
        sns.ecdfplot(tf.squeeze(res["init_matrix"][hyp]), ax=axs[i], color="orange")
        axs[i].axline((-2,0), (2,1), color="black", linestyle="dashed")
        axs[i].set_title(f"{hyp}") 
    fig.suptitle("initialization distributions")
    plt.show()

plot_inits(elicit.results)
../_images/cd08fbe7cc624464344b65abf89883c1fba754aa1f66047811d45126cf1264a8.png

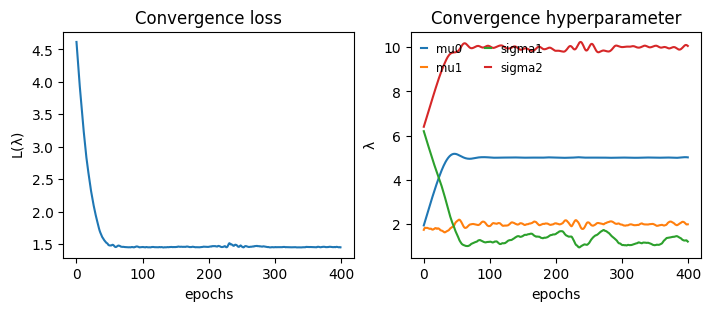
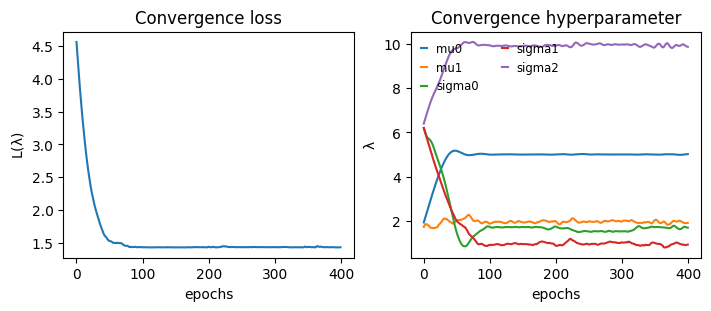
Convergence#

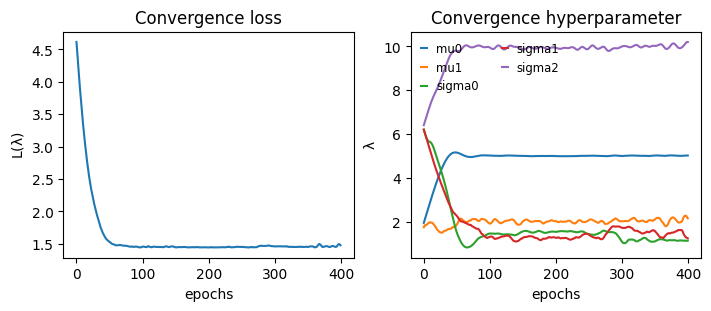
def plot_convergence(hist):
    _, axs = plt.subplots(1,2, constrained_layout=True, figsize=(7,3), sharex=True)
    axs[0].plot(hist["loss"])
    for k in hist["hyperparameter"]:
        axs[1].plot(hist["hyperparameter"][k], label=k)
        axs[1].legend(handlelength=0.5, fontsize="small", frameon=False, ncol=2)
    axs[0].set_title("Convergence loss")
    axs[1].set_title("Convergence hyperparameter")
    axs[0].set_ylabel(r"$\mathcal{L}(\lambda)$")
    axs[1].set_ylabel(r"$\lambda$")
    [axs[i].set_xlabel("epochs") for i in range(2)]
    plt.show()

plot_convergence(hist)
../_images/eda0a9688f3bdb2dc3c81b0bfbb296a731d024c1e3de7da6580dae5c044932e3.png

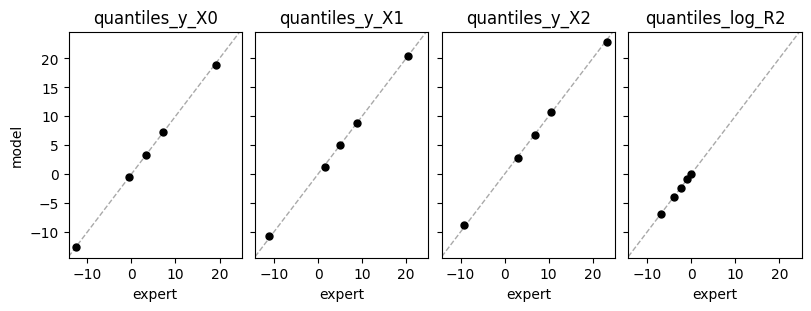
Expert expectations#

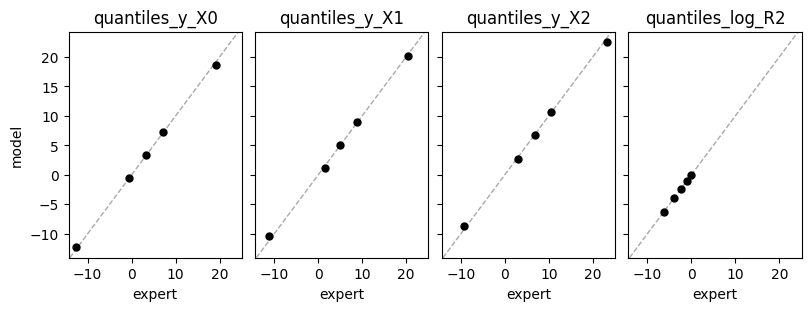
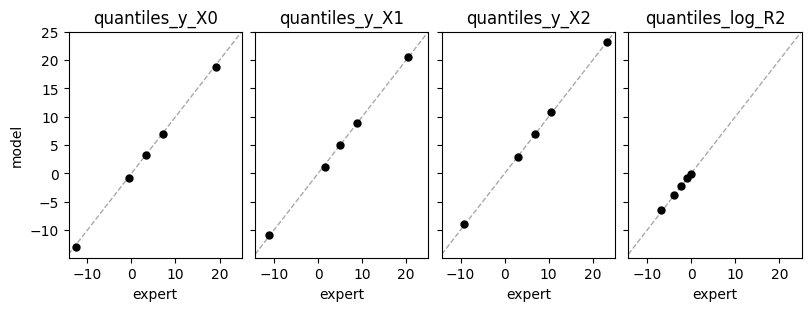
def plot_expert_data(res):
    _, axs = plt.subplots(1,4, constrained_layout=True, figsize=(8,3), sharex=True, sharey=True)
    for j,key in enumerate(res["expert_elicited_statistics"]):
        axs[j].axline((0,0), slope=1, color="darkgrey", linestyle="dashed", lw=1)
        axs[j].plot(res["expert_elicited_statistics"][key][0,:], 
                     tf.reduce_mean(res["elicited_statistics"][key],0), "o", ms=5, color="black")
        axs[j].set_title(key)
        axs[j].set_xlabel("expert")
    axs[0].set_ylabel("model")
    plt.show()

plot_expert_data(elicit.results)
../_images/3e76c209c8a8165a291fc5d6701272356578fd2b349226f0535ae3d37e3dfd89.png

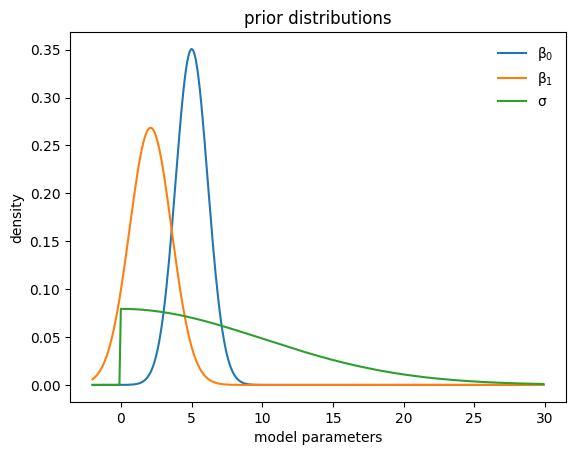
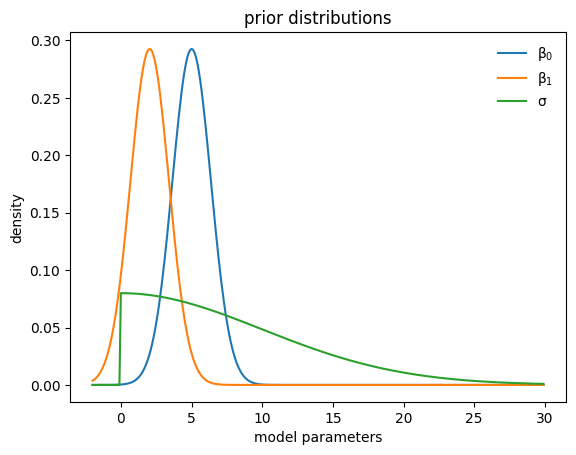
Learned priors#

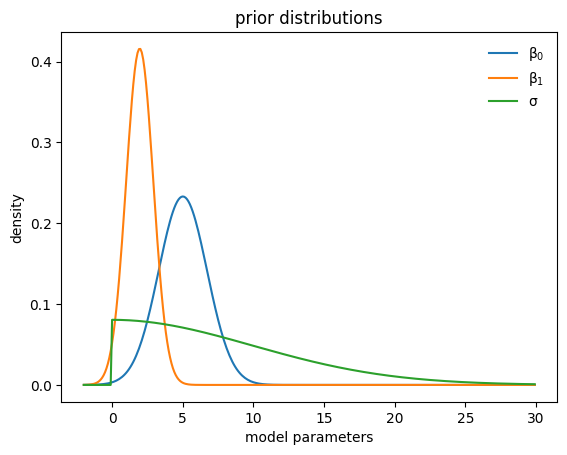
def plot_priors(hist, shared=False):
    mu0=tf.reduce_mean(hist["hyperparameter"]["mu0"][-30:])
    if shared:
        sigma0=tf.reduce_mean(hist["hyperparameter"]["sigma1"][-30:])
    else:
        sigma0=tf.reduce_mean(hist["hyperparameter"]["sigma0"][-30:])
    mu1=tf.reduce_mean(hist["hyperparameter"]["mu1"][-30:])
    sigma1=tf.reduce_mean(hist["hyperparameter"]["sigma1"][-30:])
    sigma2=tf.reduce_mean(hist["hyperparameter"]["sigma2"][-30:])
    
    x=tf.range(-2., 30., 0.1)
    y0=tfd.Normal(mu0,sigma0).prob(x)
    y1=tfd.Normal(mu1,sigma1).prob(x)
    y2=tfd.HalfNormal(sigma2).prob(x)
    
    plt.plot(x,y0, label=r"$\beta_0$")
    plt.plot(x,y1, label=r"$\beta_1$")
    plt.plot(x,y2, label=r"$\sigma$")
    plt.legend(frameon=False)
    plt.ylabel("density")
    plt.xlabel("model parameters")
    plt.title("prior distributions")
    plt.show()

plot_priors(hist)
../_images/bbecaa02a793d52ac7d9a440d2a1555a8940355a1d5dd98f6d2c702678bda4ff.png

Add-on: Shared parameters#

parameters_shared=[
        el.parameter(
            name="beta0",
            family=tfd.Normal,
            hyperparams=dict(
                loc=el.hyper("mu0"),
                scale=el.hyper("sigma1", lower=0, shared=True)
                )
        ),
        el.parameter(
            name="beta1",
            family=tfd.Normal,
            hyperparams=dict(
                loc=el.hyper("mu1"),
                scale=el.hyper("sigma1", lower=0, shared=True)
                )
        ),
        el.parameter(
            name="sigma",
            family=tfd.HalfNormal,
            hyperparams=dict(
                scale=el.hyper("sigma2", lower=0)
                )
        ),
    ]

elicit_shared = el.Elicit(
    model=model,
    parameters=parameters_shared,
    targets=targets,
    expert=expert,
    optimizer=el.optimizer(
        optimizer=tf.keras.optimizers.Adam,
        learning_rate=0.1,
        clipnorm=1.0
        ),
    trainer=el.trainer(
        method="parametric_prior",
        name="toy2",
        seed=1,
        epochs=400
    ),
    initializer=el.initializer(
        method="sobol",
        loss_quantile=0,
        iterations=32,
        distribution=el.initialization.uniform(
            radius=2.,
            mean=0.
            )
    )
)

hist_shared = elicit_shared.fit(save_dir=None)

Initialization

100%|██████████| 32/32 [00:06<00:00,  5.21it/s]

 
Training

100%|██████████| 400/400 [02:44<00:00,  2.44it/s]

Results#

Initialization of hyperparameters#

plot_inits(elicit_shared.results)
../_images/b8b830c1c202389cd82f972c74c39efd9959ceeb23b0d196d0a1c8e69bb446ee.png

Convergence#

plot_convergence(hist_shared)
../_images/4e1525d6037c1f0a57fa3687711fc3e5717255171705a777c64a2647bcf94618.png

Expert expectations#

plot_expert_data(elicit_shared.results)
../_images/93d0c50a7decc5a5911e0e53cb0f9a1737f708c409666ffd5ae0a2b81e93b299.png

Learned priors#

plot_priors(hist_shared, shared=True)
../_images/c8c5344c173d4f06262607e8a7e152c2d66e8790fcc61e0d895a0f5f91dbc92f.png

Add-on: Use expert data as input#

expert_dat = {
    "quantiles_y_X0": [-12.5, -0.6, 3.3, 7.1, 19.1],
    "quantiles_y_X1": [-11.2, 1.5, 5.0, 8.8, 20.4],
    "quantiles_y_X2": [-9.3, 3.1, 6.8, 10.5, 23.3],
    "quantiles_log_R2": tf.math.log([0.001, 0.02, 0.09, 0.41, 0.96]).numpy()
}

# define expert data
expert=el.expert.data(dat = expert_dat)

elicit_dat = el.Elicit(
    model=model,
    parameters=parameters,
    targets=targets,
    expert=expert,
    optimizer=el.optimizer(
        optimizer=tf.keras.optimizers.Adam,
        learning_rate=0.1,
        clipnorm=1.0
        ),
    trainer=el.trainer(
        method="parametric_prior",
        name="toy2",
        seed=1,
        epochs=400
    ),
    initializer=el.initializer(
        method="sobol",
        loss_quantile=0,
        iterations=32,
        distribution=el.initialization.uniform(
            radius=2.,
            mean=0.
            )
        )
)

hist_dat = elicit_dat.fit(save_dir=None)

Initialization

100%|██████████| 32/32 [00:05<00:00,  6.01it/s]

 
Training

100%|██████████| 400/400 [02:32<00:00,  2.62it/s]

Results#

Initialization of hyperparameters#

plot_inits(elicit_dat.results)
../_images/cd08fbe7cc624464344b65abf89883c1fba754aa1f66047811d45126cf1264a8.png

Convergence#

plot_convergence(hist_dat)
../_images/d6584cc5ae5f65b74ffbb36416c63f1a909ed0fa338f1a0b72144fe572b24706.png

Expert expectations#

plot_expert_data(elicit_dat.results)
../_images/f73414964e82d3d98c03d677dd9ab818ebd14aec11dfb9260cd3a28f50ca8b39.png

Learned priors#

plot_priors(hist_dat)
../_images/7f9cb5fd194863ed4b73e762d12f7f48773b05f759c8b579ba1f719dea9f7ef5.png